LDPC码是一种低密度奇偶校验码。本文将简单记录关于纠错码以及LDPC编、译码过程的学习。
参考网页:
https://zhuanlan.zhihu.com/p/514670102
https://blog.csdn.net/qq_37654178/article/details/120458583
纠错码
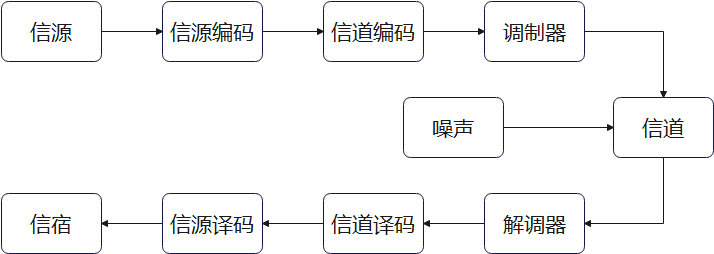
在一个典型的数字通信系统中,信源信号经过信源编码、信道编码、调制后进入信道。为了对抗信道中的噪声干扰,在传送时需要在信道编码中使用纠错码技术。
纠错码的核心
发送方为信号增加冗余信息,使接收方能检测和纠正传输中可能发生的错误。但纠错能力有限。
优点:可以纠正部分错误,不需要重发数据。 缺点:冗余信息增加了信道开销,浪费了部分带宽资源。
原理:在信源的输出上增加监督/纠错位,增加通信可靠性。
LDPC
Low Density Parity Check Code,低密度奇偶校验码。是一种(n,k)线性分组码,错误纠正能力接近香农极限。
编码原理
通过生成矩阵计算LDPC码,通过校验矩阵完成纠错。以(6,3)分组码为例。
原码\[ s=(c1,c2,c3)\] 生成矩阵\[ G= \begin{pmatrix} 1&0&0&1&0&1 \\ 0&1&0&1&1&1 \\ 0&0&1&0&1&1 \end{pmatrix}\\\]
LDPC码 \(C(s)=s\cdot G\)
校验矩阵\[H= \begin{pmatrix} 1&1&0&1&0&0 \\ 0&1&1&0&1&0 \\ 1&0&1&0&0&1 \end{pmatrix}\\\]
\(HC_{T}(s)=0\)
校验矩阵和生成矩阵一一对应-->可以用只讨论校验矩阵。
用Tanner图表示
图中包含6个变量节点和3个校验节点。变量节点对应纠错码的各个码位,校验节点负责处理信号并输出结果。类似神经网络,校验节点可以表示校验方程。
比特翻转算法-硬判决
对信道做出01判决,只有01参与运算。简单,但是性能较差。
- 首先校验零向量\(s=Hc^T\)
- 对于c对每个元素,计算结果错误的方程数量\(f_n=\sum_{m=1}^3(s_m\cdot h_{mn})\)
- 如果\(f_n\)超过设定值则翻转元素\(c_n\),重新校验
硬判决举例
\(s=(1 1 0)\),编码结果\(C(s)=(1 1 0 0 1 1)\) ,接收信号\(c=(010011)\),校验矩阵\[H= \begin{pmatrix} 1&1&0&1&0&0 \\ 0&1&1&0&1&0 \\ 1&0&1&0&0&1 \end{pmatrix}\\\]
- \(s=(101)\)不是零向量,传输错误
- 计算\(f=(211101)\)
- 翻转\(c_1\)
- 重新校验,s为零向量,译码成功。
置信传播算法-软判决
使用概率判决信息,提高纠错性能。
在本算法中使用对数似然比来表征概率,假设某码位是 0 的概率为\(p\) ,则其为1的概率就是 \(1-p\) ,此时用对数似然比ln(p/1-p)来表示该位的电平概率,可以起到一个放大概率的作用。
初始化先验概率:用码位的正确传送概率计算对数似然比\(ln(1-p/p)\)或\(ln(p/1-p)\)来表征码位倾向,结果越正,码位为 0 的概率越大;结果越负,码位为 1 的概率越大。 初始化变量矩阵M:如果c的位为1,H对应列的1改为1的对数似然比;c的位为0,H对应列的1改为0的对数似然比。表示信道输出中每一个码位的电平概率。
更新变量矩阵M:用对数似然比结合E矩阵的信息。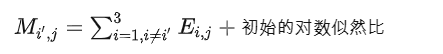
更新校验矩阵E:对于某一码位,参考校验方程中其他相关码位的意见,修改自己的电平概率。再将每一列相加,得到确切的电平概率作为后验概率向量。加入约束条件后更能表征电平概率
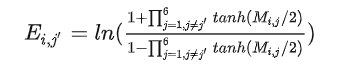
计算后验概率:将\(E\)矩阵求列和,并加上初始对数似然比,得到后验概率。
比特判决:负数判决为1,正数判决为0。
校验:根据H矩阵对判决结果进行校验。
软判决举例
比如\(c=(110111),p=0.8\),可以计算得到对于1的对数似然比为-1.386,对于0为1.386。 校验矩阵\[H= \begin{pmatrix} 1&1&0&1&0&0 \\ 1&0&1&0&1&0 \\ 0&1&1&0&0&1 \\ \end{pmatrix}\\\]
变量矩阵\[M= \begin{pmatrix} -1.386&-1.386&0&-1.386&0&0\\ -1.386&0&1.386&0&-1.386&0 \\ 0&-1.386&1.386&0&0&-1.386 \\ \end{pmatrix}\\\]
校验矩阵\[E= \begin{pmatrix} 0.7538&0.7538&0&0.7538&0&0\\ -0.7538&0&0.7538&0&-0.7538&0 \\ 0&-0.7538&0.7538&0&0&-0.7538\\ \end{pmatrix}\\\]
后验概率为\((-1.386,-1.386,2.894,-0.632,-2.140,-2.140)\)
根据后验概率得到判决输出为\((110111)\)
校验不通过,重新计算\(M\)和\(E\)矩阵,直到判决正确。